Đề bài
Một xe ô tô chở khách du lịch có sức chứa tối đa là 16 hành khách. Trong một khu du lịch, một đoàn khách gồm 22 người đang đi bộ và muốn thuê xe về khách sạn. Lái xe đưa ra thỏa thuận với đoàn khách du lịch như sau: Nếu một chuyến xe chở x (người) thì giá tiền cho mỗi người là $\dfrac{\left( {40 - x} \right)^{2}}{2}$ (nghìn đồng). Với thoả thuận như trên thì lái xe có thể thu được nhiều nhất bao nhiêu triệu đồng từ một chuyến chở khách (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải
+ Gọi $f(x)$ là lợi nhuận mà lái xe có thể thu về khi chở $x$ người, đặt điều kiện cho ẩn.
+ Tính được $f(x) = \dfrac{1}{2}x{{\left( 40-x \right)}^{2}}$, tìm giá trị lớn nhất của $f(x)$ với $0<x\le 16$, từ đó rút ra kết luận
Lời giải chi tiết
Gọi $f(x)$ là lợi nhuận mà lái xe có thể thu về khi chở $x$ người $\left( x\in {{\mathbb{N}}^{*}} \right)$ trong chuyến xe đó.
Khi đó, $f\left( x \right)=\dfrac{1}{2}x{{\left( 40-x \right)}^{2}}$ với $0<x\le 16$.
Ta có: $f'\left( x \right)=\dfrac{1}{2}\left[ {{\left( 40-x \right)}^{2}}-2x\left( 40-x \right) \right]=\dfrac{1}{2}\left( 40-x \right)\left( 40-3x \right)$.
$f'\left( x \right)=0\Leftrightarrow x=\dfrac{40}{3}$ (do $0<x\le 16$). Vì $13<\dfrac{40}{3}<14$ nên ta có bảng biến thiên:
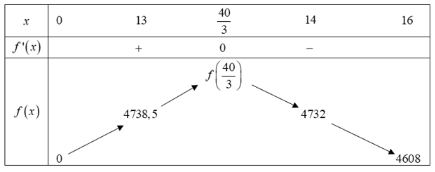
Theo bảng biến thiên ta có: $\underset{\left( 0;\ 16 \right]}{\mathop{\max }}\,f\left( x \right)=4738,5$ (nghìn đồng).
Vậy người lái xe đó thu được nhiều lợi nhuận nhất khoảng 4,74 triệu đồng từ một chuyến xe chở 13 khách.
Chú ý khi giải
+ Điều kiện của ẩn: x là số tự nhiên $0<x\le 16$, nên khi tìm giá trị lớn nhất, cần tìm giá trị lớn nhất đạt được tại giá trị của x là số tự nhiên.
Cách giải bài toán tối ưu hóa đơn giản:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số $Q=Q\left( x \right)$.
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số $Q=Q\left( x \right)$ bằng các phương pháp đã biết và kết luận.
📌 Ứng dụng của bài toán tối ưu hóa trong thực tiễn: Bài toán tối ưu hóa giúp chúng ta giải quyết những vẫn đề trong cuộc sống như tối đa hóa diện tích, khối lượng, lợi nhuận, cũng như tối thiểu hóa khoảng cách, thời gian, chi phí.