Đề bài
Một hộ làm nghề dệt vải tơ tằm sản xuất mỗi ngày được $x$ mét vải lụa ($1 \leq x \leq 18$). Tổng chi phí để sản xuất $x$ mét vải lụa (tính bằng ngàn đồng) cho bởi hàm chi phí $C(x) = x³ - 3x²–20x + 500$. Giả sử hộ gia đình này bán hết sản phẩm ở mỗi ngày với giá 220 ngàn đồng/mét. Tính số tiền (đơn vị ngàn đồng) lợi nhuận tối đa mà hộ gia đình này có thể nhận được.
Phương pháp giải
Lập biểu thức tính lợi nhuận thu được khi bán $x$ mét vải lụa.
Khảo sát hàm số để xác định lợi nhuận lớn nhất.
Lời giải chi tiết
Số tiền thu về khi bán $x$ mét vài lụa là: $220x$.
Lợi nhuận thu được khi bán $x$ mét vải lụa là:
$L(x)=220 x-\left(x^3-3 x^2-20 x+500\right)=-x^3+3 x^2+240 x-500$
Xét hàm số:
$L(x)=-x^3+3 x^2+240 x-500$ vớ $x \in[1 ; 18]$
$L^{\prime}(x)=-3 x^2+6 x+240=0$
$\Leftrightarrow\left[\begin{array}{l}x=10 \in[1 ; 18] \\ x=-8 \notin[1 ; 18]\end{array}\right.$
Bảng biến thiên:
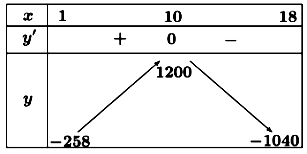
Vậy hộ làm nghề dệt này thu được lợi nhuận tối đa trong một ngày là 1200 nghìn đồng khi sản xuất 10 mét vài lụa trong một ngày.
1. Hàm số bậc ba
- Hàm chi phí $C(x)=x^3-3 x^2-20 x+500$ có dạng hàm bậc ba, và ta cần tối ưu hóa lợi nhuận bằng cách tìm giá trị lớn nhất của hàm lợi nhuận.
2. Hàm lợi nhuận
- Lợi nhuận được tính theo công thức:
$L(x)=$ Doanh thu - Chi phí
Trong đó:
- Doanh thu: $R(x)=220x$ (do bán được $x$ mét với giá 220 ngàn đồng/mét)
- Chi phí: $C(x)=x^3-3 x^2-20 x+500$.
3. Tìm giá trị lớn nhất của hàm số
Khảo sát hàm Lợi nhuận để xác định lợi nhuận lớn nhất.
- Tối ưu hóa sản xuất: Bài toán giúp hộ gia đình xác định mức sản xuất sao cho lợi nhuận đạt mức cao nhất.
- Quản lý chi phí và giá bán: Biết cách tính Iợi nhuận giúp doanh nghiệp điều chỉnh giá bán và kiểm soát chi phí sản xuất.
- Ứng dụng trong kinh tế và kinh doanh: Các doanh nghiệp sản xuất thực tế cunng sử dụng các mô hình hàm số bậc hai để phân tích lợi nhuận, điều chỉnh quy trình sản xuất nhằm đạt hiệu quả cao nhất.