Đề bài
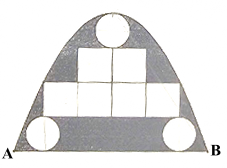
Một cửa vòm có dạng hình parabol được lắp các tấm kính hình tròn đường kính 1 m và các tấm kính hình vuông có cạnh 1 m như hình vẽ. Phần còn lại của cửa được sơn màu trang trí với mức giá 1,2 triệu đồng/$m^{2}$. Chi phí sơn màu là bao nhiêu triệu đồng (kết quả làm tròn đến hàng phần chục)?
Phương pháp giải
Gắn hệ trục tọa độ tìm parabol và diện tích.
Lời giải chi tiết
Gắn hệ trục tọa độ như hình vẽ
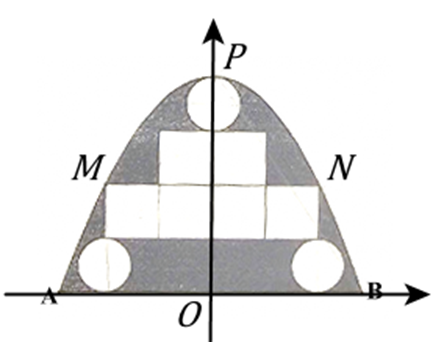
Từ đường tròn đường kính 1 và hình vuông cạnh 1 suy ra $OP = 4,MN = 4$
$\Rightarrow P\left( {0,4} \right);M\left( { - 2,2} \right),N\left( {2,2} \right)$
Ta có parabol đi qua P, M, N nên có phương trình $y = - \dfrac{1}{2}{x^2} + 4$
Xét $- \dfrac{1}{2}{x^2} + 4 = 0 \Leftrightarrow x = \pm 2\sqrt 2 \Rightarrow A\left( { - 2\sqrt 2 ,0} \right),B\left( {2\sqrt 2 ,0} \right)$
Diện tích phần kính là ${S_1} = \pi .0,{5^2}.3 + 6.1.1 = 0,75\pi + 6 (m^2)$.
Diện tích parabol tạo với Ox là $S = \int\limits_{ - 2\sqrt 2 }^{2\sqrt 2 } {\left( { - \dfrac{1}{2}{x^2} + 4} \right)} dx$
Vậy cho phí sơn màu là $1,2.\left( {S - {S_1}} \right) = 8,1$ triệu đồng.
Đáp án: 8,1
+ Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $f(x)$ và $g(x)$ và hai đường thẳng $x = a$, $x = b$: Diện tích S của hình phẳng giới hạn bởi hai đồ thị của hai hàm số $f(x)$ và $g(x)$ liên tục trên đoạn $[a; b]$ và hai đường thẳng $ x = a$, $x = b$ được tính bằng công thức $S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|}\ dx$.
Chú ý: Nếu hiệu $f\left( x \right)-g\left( x \right)$ không đổi dấu trên đoạn $[a; b]$ thì $\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|}\ dx=\left| \int\limits_{a}^{b}{\left[ f\left( x \right)-g\left( x \right) \right]}\ dx \right|$
📌 Ứng dụng của tích phân: Tích phân có nhiều ứng dụng trong nhiều lĩnh vực:
+ Trong vật lí:
- Tính quãng đường vật chuyển động nếu biết vận tốc theo thời gian.
- Tính công – năng lượng: Tích phân lực theo quãng đường để tính công.
- Tính mô men quán tính, trọng tâm, khối lượng: Tích phân phân bố khối lượng theo hình học.
- Dòng điện – từ: Tích phân để tính điện tích, dòng điện qua một diện tích.
+ Trong kinh tế:
- Tính tổng lợi nhuận hoặc chi phí: Nếu biết lợi nhuận/chi phí biên theo thời gian/sản lượng.
- Tính lũy kế của một đại lượng: Ví dụ: Tích lũy lãi suất, dân số, doanh thu qua thời gian.
+ Trong Sinh học - Y học:
- Mô hình hóa tăng trưởng: Dùng tích phân để tính tổng số sinh vật trong một khoảng thời gian.
- Dược động học: Tính lượng thuốc trong cơ thể qua thời gian.
+ Tính diện tích của hình phẳng giới hạn giữa đồ thị hàm và trục hoành, ...
+ Tính thể tích vật thể: Dùng tích phân để tính thể tích khối tròn xoay, thể tích vật thể có mặt cắt thay đổi.
+ Tính độ dài đường cong: Tính độ dài cung của một đường cong bằng công thức tích phân.