Đề bài
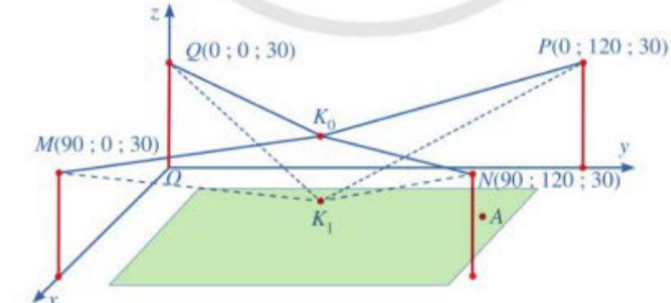
Người ta cần lắp một camera phía trên sân bóng để phát sóng truyền hình một trận bóng đá, camera có thể di động để luôn thu được hình ảnh rõ nét về diễn biến trên sân. Các kĩ sư dự định trồng bốn chiếc cột cao $30\text{m}$ và sử dụng hệ thống cáp gắn vào bốn đầu cột để giữ camera ở vị trí mong muốn. Mô hình thiết kế được xây dựng như sau: Trong hệ trục toạ độ $Oxyz$ (đơn vị độ dài trên mỗi trục là $1\text{m})$, các đỉnh của bốn chiếc cột lần lượt là các điểm $M\left( {90;0;30} \right)$, $N\left( {90;120;30} \right),P\left( {0;120;30} \right),Q\left( {0;0;30} \right)$.
Giả sử $K_{0}$ là vị trí ban đầu của camera có cao độ bằng 25 và $K_{0}M = K_{0}N = K_{0}P = K_{0}Q$. Để theo dõi quả bóng đến vị trí $A$, camera được hạ thấp theo phương thẳng đứng xuống điểm $K_{1}$ cao độ bằng 19.
Tọa độ của vectơ $\overset{\rightarrow}{K_{0}K_{1}} = \left( {a;b;c} \right)$với $a,b,c$ là các số thực. Tính $P = a + b + 3c$?
Phương pháp giải
Bước 1: tìm cao độ của điểm ${{K}_{0}}$
Bước 2: Giải phương trình ${{K}_{0}}N={{K}_{0}}M$ để tìm được tung độ và hoành độ của ${{K}_{0}}$ . Từ đó suy ra tọa độ của ${{K}_{1}}$
Bước 3: Tìm tọa độ $\overrightarrow{{{K}_{0}}{{K}_{1}}}$
Lời giải chi tiết
Giả sử ${{K}_{0}}$ là vị trí ban đầu của camera có cao độ bằng 25. Nên ${{K}_{0}}\left( {{x}_{{{K}_{0}}}},{{y}_{{{K}_{0}},}}25 \right)$
Ta có $\overrightarrow{{{K}_{0}}M}(90-{{x}_{{{K}_{0}}}},-y{}_{{{K}_{0}}},5)$ và $\overrightarrow{{{K}_{0}}N}(90-{{x}_{{{K}_{0}}}},120-y{}_{{{K}_{0}}},5)$ mà ${{K}_{0}}N={{K}_{0}}M$.
Giải ${{K}_{0}}N={{K}_{0}}M$.
$\sqrt{{{\left( 90-{{x}_{{{K}_{0}}}} \right)}^{2}}+{{y}_{{{K}_{0}}}}^{2}+{{5}^{2}}}=\sqrt{{{\left( 90-{{x}_{{{K}_{0}}}} \right)}^{2}}+{{\left( 120-{{y}_{{{K}_{0}}}} \right)}^{2}}+{{5}^{2}}}$
$\overrightarrow{{{K}_{0}}M}(90-{{x}_{{{K}_{0}}}},-y{}_{{{K}_{0}}},5)$ và $\overrightarrow{{{K}_{0}}Q}(-{{x}_{{{K}_{0}}}},-{{y}_{{{K}_{0}}}},5)$ mà ${{K}_{0}}M={{K}_{0}}Q$
\[\sqrt{{{\left( 90-{{x}_{{{K}_{0}}}} \right)}^{2}}+{{y}_{{{K}_{0}}}}^{2}+{{5}^{2}}}=\sqrt{{{x}_{{{K}_{0}}}}^{2}+{{y}_{{{K}_{0}}}}^{2}+{{5}^{2}}}\]
$\Rightarrow {{x}_{{{K}_{0}}}}=45$
Vậy $M\left( 45,60,25 \right)$ .
Camera được hạ thấp theo phương thẳng đứng xuống điểm
cao độ bằng 19 nên $N\left( 45,60,19 \right)$
Tọa độ $\overrightarrow{{{K}_{0}}{{K}_{1}}}(0,0,-15)\Rightarrow a=0,\,\,b=0,\,\,\,c=-15\Rightarrow a+b+c=-15$
Đáp số 15