Đề bài
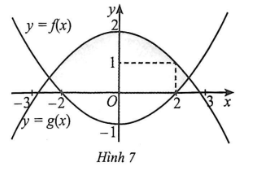
Bạn Hải nhận thiết kế logo hình con mắt (phần được tô đậm) cho một cơ sở y tế. Logo là hình phẳng giới hạn bởi hai parabol $y = f\left( x \right)$ và $y = g\left( x \right)$ như Hình 7 (đơn vị trên mỗi trục toạ độ là decimét). Bạn Hải cần tính diện tích của logo để báo giá cho cơ sở y tế đó trước khi kí hợp đồng. Diện tích của logo là bao nhiêu decimet vuông (làm tròn kết quả đến hàng phần mười).
Phương pháp giải
+ Tìm hàm số $f(x)$ và $g(x)$.
+ Viết phương trình hoành độ giao điểm của $f(x)$ và $g(x)$, tìm các giá trị $x$.
+ Sử dụng công thức tích phân để tính diện tích hình phẳng được giới hạn bởi hai đồ thị hàm số và hai đường thẳng để tính diện tích logo.
Lời giải chi tiết
Gọi parabol $y=f(x)$ có dạng $f(x)=a x^{2}+b x+c$ ($a$ khác 0). Parabol $y=f(x)$ nhận $Oy$ làm trục đối xứng nên ta có $\dfrac{-b}{2 a}=0 \Leftrightarrow b=0$. Lại có đồ thị hàm số $y=f(x)$ đi qua điểm $(0 ;-1)$ và điểm $(2 ; 0)$ nên:
\(\left\{ \begin{array}{l} -1 = a.0^2 + c \\ 0 = a.2^2 + c\end{array} \right.\) $ \Leftrightarrow a=\dfrac{1}{4}, c=-1$ (thỏa mãn).
Vậy parabol $y=f(x)=\dfrac{1}{4} x^{2}-1$.
-Gọi parabol $y=g(x)$ có dạng $g(x)=a x^{2}+bx+c$ ($a$ khác 0). Parabol $y=g(x)$ nhận $Oy$ làm trục đối xứng nên ta có $\dfrac{-b}{2 a}=0 \Leftrightarrow b=0$. Lại có đồ thị hàm số $y=g(x)$ đi qua điểm $(2; 1)$ và điểm $(0 ; 2)$.
Do đó: \(\left\{ \begin{array}{l} 2 = a.0^2 + c \\ 1 = a.2^2 + c\end{array} \right.\) $ \Leftrightarrow a=\dfrac{-1}{4}, c = 2$ (thỏa mãn).
Vậy parabol $y=g(x)=\dfrac{-1}{4} x^{2} + 2$.
- Phương trình hoành độ giao điểm của $f(x)$ và $g(x)$ là:
$$\dfrac{1}{4} x^{2}-1=-\dfrac{1}{4} x^{2}+2 \Leftrightarrow x=\sqrt{6} \text { hoặc } x=-\sqrt{6} \text {. }$$
Khi đó, diện tích của logo là:
$$\begin{aligned}S & =\int_{-\sqrt{6}}^{\sqrt{6}}\left[\left(-\dfrac{1}{4} x^{2}+2\right)-\left(\dfrac{1}{4} x^{2}-1\right)\right] \mathrm{d} x \\& =\int_{-\sqrt{6}}^{\sqrt{6}}\left(3-\frac{1}{2} x^{2}\right) \mathrm{d} x=\left.\left(3 x-\frac{x^{3}}{6}\right)\right|_{-\sqrt{6}} ^{\sqrt{6}}=4 \sqrt{6} \approx 9,8\left(\mathrm{dm}^{2}\right) .\end{aligned}$$
+ Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng $x = a$, $x = b$: Diện tích S của hình phẳng giới hạn bởi hai đồ thị của hai hàm số $f(x)$ và $g(x)$ liên tục trên đoạn $[a; b]$ và hai đường thẳng $ x = a$, $x = b$ được tính bằng công thức $S=\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|}\ dx$.
Chú ý: Nếu hiệu $f\left( x \right)-g\left( x \right)$ không đổi dấu trên đoạn $[a; b]$ thì $\int\limits_{a}^{b}{\left| f\left( x \right)-g\left( x \right) \right|}\ dx=\left| \int\limits_{a}^{b}{\left[ f\left( x \right)-g\left( x \right) \right]}\ dx \right|$
📌 Ứng dụng của tích phân: Tích phân có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau:
+ Tính diện tích hình phẳng: Tích phân được dùng để tính diện tích các hình có hình dạng phức tạp.
+ Tính thể tích vật thể: Khi quay một hình phẳng quanh một trục, ta có thể dùng tích phân để tính thể tích của vật thể quay đó.
+ Vật lí và cơ học: Nếu biết hàm số mô tả vận tốc theo thời gian, tích phân của hàm vận tốc cho ta quãng đường đi được; công của một lực thay đổi theo quãng đường có thể được tính bằng tích phân của lực theo quãng đường.
+ Sinh học và y học:
- Mô hình tăng trưởng: Mô hình tăng trưởng của quần thể, sử dụng tích phân để tính số lượng quần thể qua thời gian dựa trên tốc độ tăng trưởng biến thiên.
- Phân bố liều lượng thuốc: Tích phân giúp xác định liều lượng thuốc tối ưu khi xét đến tốc độ hấp thu và bài tiết của cơ thể, từ đó đảm bảo hiệu quả điều trị và an toàn cho bệnh nhân.
+ Kinh tế, tài chính:
- Tính lãi kép và dự báo kinh tế: Tích phân có thể được sử dụng trong các mô hình kinh tế để tính tích lũy theo thời gian như lãi kép hay tổng giá trị của các dòng tiền không liên tục.
- Phân tích rủi ro: Trong kinh tế lượng, tích phân giúp tính xác suất liên tục của các biến ngẫu nhiên, hỗ trợ trong việc phân tích và dự báo rủi ro tài chính.
📊 Thực tế bài toán: Để tính được diện tích logo mà bạn Hải thiết kế, ta sử dụng ứng dụng của tích phân trong việc tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và hai đường thẳng $x = a$, $x = b$.