Đề bài
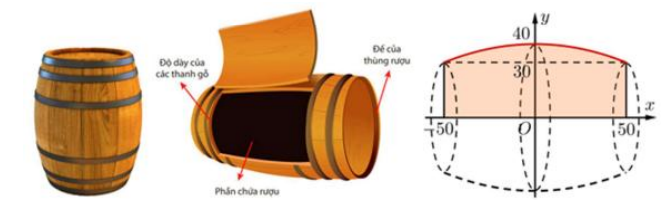
Một thùng rượu vang có dạng khối tròn xoay với bán kính mặt đáy và mặt ở trên là 33$cm$, bán kính mặt cắt ở chính giữa thùng là 43$cm$. Chiều cao của thùng rượu là 112$cm$, bao gồm phần thân thùng rượu, hai đế đỡ thùng rượu (mỗi đế cao 3$cm$) và thùng rượu được ghép từ các thanh gỗ sồi với độ dày mỗi thanh gỗ là 3$cm$. Phần bên trong thùng rượu có dạng một khối tròn xoay tạo thành khi quay một phần của parabol $(P):y = ax^{2} + bx + c$ quanh trục hoành như hình sau:
Phương pháp giải
a) Xác định các điểm thuộc Parabol và trục đối xứng
b) Xác định các điểm thuộc Parabol và trục đối xứng
c) Tính diện tích bằng tích phân
d) Tính thể tích bằng tích phân
Lời giải chi tiết
a) Đúng: Phương trình parabol: $y = ax^{2} + bx + c\left( {a \neq 0} \right)$ đi qua điểm A(0;40), B(50;30) và trục đối xứng x = 0
$\left. \Rightarrow\left\{ \begin{array}{l} {40 = c} \\ {30 = 50^{2}a + 50b + c} \\ {\dfrac{- b}{2a} = 0} \end{array} \right.\Leftrightarrow\left\{ \begin{array}{l} {a = - \dfrac{1}{250}} \\ {b = 0} \\ {c = 40} \end{array} \right.\Rightarrow y = \dfrac{- 1}{250}x^{2} + 40 \right.$
b) Đúng
c) Sai: Diện tích thiết diện phần chứa rượu là: $S = 2{\int\limits_{- 50}^{50}{\left( {\dfrac{- 1}{250}x^{2} + 40} \right)dx = \dfrac{22000}{3}\left( {cm^{2}} \right) = \dfrac{11}{15}\left( m^{2} \right)}}$
d) Đúng: Thể tích phần chứa rượu là: $V = \pi{\int\limits_{- 50}^{50}{\left( {\dfrac{- 1}{250}x^{2} + 40} \right)^{2}dx}} \approx 425162(cm^{3}) = 425,16(l)$