Đề bài
Một cái hồ lô trang trí được thiết kế phần chứa nước có thể tích bằng với thể tích của một vật thể $(V)$ trong không gian. Biết rằng, điểm $M$ thuộc $(V)$ khi và chỉ khi $MA < \sqrt{2}dm$ hoặc$MB < \sqrt{5}dm$; trong đó $A$ và $B$ là hai điểm cố định, $AB = 3dm$. Thể tích phần chứa nước của hồ lô đó là bao nhiêu lít? (làm tròn kết quả đến hàng phần chục)

Phương pháp giải
Thể tích của hồ lô $V={{V}_{1}}+{{V}_{2}}$. Trong đó:
${{V}_{1}}=\pi \int\limits_{a}^{b}{f(x)dx}$ với $f\left( x \right)$ là phương trình đường tròn tâm $B$, ta tìm tọa độ điểm $H$ để xác định cận trên của tích phân.
${{V}_{2}}=\pi \int\limits_{a}^{b}{g(x)dx}$ với $g(x)$ là phương trình đường tròn tâm $A$, tọa độ điểm $H$ là cận dưới của tích phân.
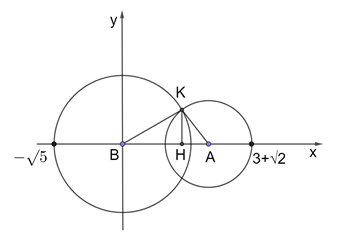
Gọi $K$ là giao điểm của 2 đường tròn, $H$ là hình chiếu của $K$ xuống $Ox$.
Lời giải chi tiết
Ta đặt hệ trục tọa độ như sau:
$B(0;0)$; $A(3;0)$
Thể tích của hồ lô là thể tích của phần màu cam cộng với thể tích của phần màu vàng , hai phần này được ngăn cách bởi đường thẳng đi qua $H$ và song song với trục $Oy$.
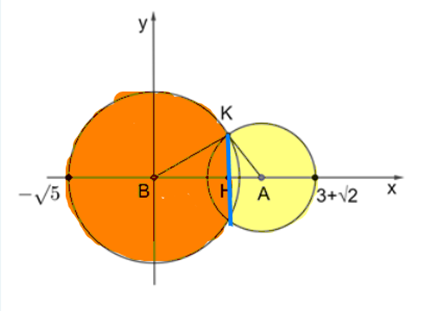
Thể tích của hồ lô $V={{V}_{1}}+{{V}_{2}}$.
Phương trình đường tròn tâm $B$: ${{x}^{2}}+{{y}^{2}}=5$$\Rightarrow {{y}^{2}}=5-{{x}^{2}}$
Phương trình đường tròn tâm $A$: ${{\left( x-3 \right)}^{2}}+{{y}^{2}}=2$${{y}^{2}}=2-{{\left( x-3 \right)}^{2}}$
Trước hết ta tính thể tích phần màu cam:
${{V}_{1}}=\pi \int\limits_{a}^{b}{f(x)dx}$ với $f\left( x \right)$ là phương trình đường tròn tâm $B$
Gọi giao điểm của hai đường tròn tâm $A$ và $B$ là $K$.
$H$ là hình chiếu của $K$ trên trục $Ox$.
Giả sử $BH=x,\,\,AH=3-x$.
Ta có: $\Delta HBK$và $\Delta HKA$ vuông tại $H$
$\Rightarrow H{{K}^{2}}=B{{K}^{2}}-B{{H}^{2}}=A{{K}^{2}}-A{{H}^{2}}$
$\Rightarrow {{\left( \sqrt{5} \right)}^{2}}-{{x}^{2}}={{\left( \sqrt{2} \right)}^{2}}-{{\left( 3-x \right)}^{2}}\Rightarrow x=2$ $\Rightarrow BH=2$.
$H{{K}^{2}}=B{{K}^{2}}-B{{H}^{2}}=5-2=1\Rightarrow HK=1$.
Suy ra tọa độ điểm $H$ là $\left( 2;0 \right)$.
Phần thể tích ${{V}_{1}}$ bị giới hạn bởi đường thẳng $x=-\sqrt{5}$ và đường thẳng $x=2$
Thể tích ${{V}_{1}}=\pi \int\limits_{-\sqrt{5}}^{2}{\left( 5-{{x}^{2}} \right)dx}\approx 46,43.$
Thể tích màu vàng:
${{V}_{2}}=\pi \int\limits_{a}^{b}{g(x)dx}$ với $g(x)$ là phương trình đường tròn tâm $A$
Biết $AB=3$ và bán kính đường tròn tâm $A$ là $\sqrt{2}$ nên phần thể tích ${{V}_{2}}$ sẽ bị giới hạn bởi đường thẳng $x=2$ và đường thẳng $x=3+\sqrt{2}$.
Thể tích ${{V}_{2}}=\pi \int\limits_{2}^{3+\sqrt{2}}{\left( 2-{{\left( x-3 \right)}^{2}} \right)dx\approx 11,18}$
Thể tích vật cần tính: $V={{V}_{1}}+{{V}_{2}}=46,43+11,18\approx 57,61.$
Vậy thể tích hồ lô là $57,6$ lít.