Đề bài
Một nhà địa chất học đang ở tại điểm $A$ trên sa mạc. Anh ta muốn đến điểm $B$ và cách $A$ một đoạn là $70\,\text{km}$. Trong sa mạc thì xe anh ta chỉ có thể di chuyển với vận tốc là $30\,\text{km/h}\text{.}$Nhà địa chất phải đến được điểm $B$ sau $2$ giờ. Vì vậy, nếu anh ta đi từ $A$ đến $B$ sẽ không thể đến đúng giờ được. May mắn thay, có một con đường nhựa song song với đường nối $A$ và $B$ và cách $AB$ một đoạn $10\,\text{km}$. Trên đường nhựa đó thì xe nhà địa chất này có thể di chuyển với vận tốc $50\,\text{km/h}$. Thời gian ngắn nhất để nhà địa chất di chuyển từ $A$ đến $B$ là bao nhiêu phút.
Phương pháp giải
+ Chia quãng đường đi được thành 3 giai đoạn:
Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)
Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)
Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).
+ Khi đó, thời gian đi từ A đến B bằng tổng thời gian đi qua ba giai đoạn trên. Do đó, tìm được hàm số biểu diễn thời gian đi được.
+ Tìm giá trị nhỏ nhất của hàm số đó và rút ra kết luận.
Lời giải chi tiết
Từ đầu bài ta có hình vẽ:
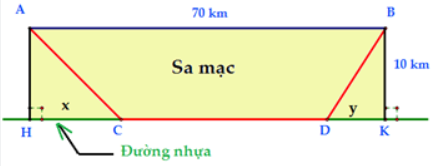
Gọi $HC=x\left( 0<x<70 \right)$ và $DK=y\left( 0<y<70 \right)$
Khi đó, $AC=\sqrt{{{10}^{2}}+{{x}^{2}}},BD=\sqrt{{{10}^{2}}+{{y}^{2}}},CD=70-\left( x+y \right)$
Suy ra:
${{t}_{AC}}=\dfrac{AC}{30}=\dfrac{\sqrt{100+{{x}^{2}}}}{30};{{t}_{BD}}=\dfrac{BD}{30}=\dfrac{\sqrt{100+{{y}^{2}}}}{30};{{t}_{CD}}=\dfrac{CD}{50}=\dfrac{70-\left( x+y \right)}{50}$
Tổng thời gian mà nhà địa chất học đi từ A đến B là:
$T={{t}_{AC}}+{{t}_{BD}}+{{t}_{DC}}$
$=\dfrac{\sqrt{100+{{x}^{2}}}}{30}+\dfrac{\sqrt{100+{{y}^{2}}}}{30}+\dfrac{\sqrt{70-\left( x+y \right)}}{50}$
$=\left( \dfrac{\sqrt{100+{{x}^{2}}}}{30}+\dfrac{35-x}{50} \right)+\left( \dfrac{\sqrt{100+{{y}^{2}}}}{30}+\dfrac{35-y}{50} \right)$
Xét $f\left( x \right)=\dfrac{\sqrt{100+{{x}^{2}}}}{30}+\dfrac{35-x}{50}$. Ta có: $f'\left( x \right)=\dfrac{x}{30\sqrt{100+{{x}^{2}}}}-\dfrac{1}{50}=0\Rightarrow x=\dfrac{15}{2}$
Suy ra: $\underset{0<x<70}{\mathop{\min }}\,f\left( x \right)=f\left( \dfrac{15}{2} \right)=\dfrac{29}{30}$.
Xét $f\left( y \right)=\dfrac{\sqrt{100+{{y}^{2}}}}{30}+\dfrac{35-y}{50}$. Tương tự ta có: $\underset{0<x<70}{\mathop{\min }}\,f\left( y \right)=f\left( \dfrac{15}{2} \right)=\dfrac{29}{30}$
Do đó, $T\ge \dfrac{29}{30}+\dfrac{29}{30}=\dfrac{29}{15}$ (giờ).
Vậy thời gian ngắn nhất để nhà địa chất di chuyển từ A đến B là: $\dfrac{29}{15}$ giờ = 116 phút.
Cách giải bài toán tối ưu hóa đơn giản:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số $Q=Q\left( x \right)$.
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số $Q=Q\left( x \right)$ bằng các phương pháp đã biết và kết luận.
📌 Ứng dụng của bài toán tối ưu hóa trong thực tiễn: Bài toán tối ưu hóa giúp chúng ta giải quyết những vẫn đề trong cuộc sống như tối đa hóa diện tích, khối lượng, lợi nhuận, cũng như tối thiểu hóa khoảng cách, thời gian, chi phí.