Đề bài
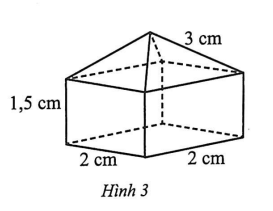
Người ta thiết kế một thiết bị kim loại có dạng như Hình 3 (giá tiền mua kim loại là 2500 đồng $/ \mathrm{cm}^{3}$ ). Thiết bị gồm 2 phần, phần dưới là khối lăng trụ tứ giác đều, phần trên là khối chóp tứ giác đều. Số tiền mua kim loại dùng để làm thiết bị đó là bao nhiêu nghìn đồng (làm tròn kết quả đến hàng đơn vị)?
Phương pháp giải
+ Tính thể tích khối lăng trụ có chiều cao $1,5cm$ và độ dài cạnh đáy $2cm$.
+ Tính độ dài đường chéo mặt đáy của khối chóp tứ giác đều, từ đó sử dụng định lý Pythagore để tính chiều cao của của khối chóp tứ giác đều.
+ Tính thể tích khối chóp tứ giác đều có độ dài cạnh đáy $2cm$ và chiều cao đã tính ở trên.
+ Thể tích thiết bị kim loại = Thể tích khối chóp tứ giác đều + Thể tích khối lăng trụ.
+ Số tiền mua kim loại dùng để làm thiết bị = Thể tích thiết bị kim loại $\cdot 2,5$ (nghìn đồng).
Lời giải chi tiết
Thể tích khối lăng trụ tứ giác đều là: $V_{1}=1,5 \cdot 2^{2}=6\left(\mathrm{~cm}^{3}\right)$.
Độ dài đường chéo mặt đáy của khối chóp tứ giác đều là: $\sqrt{2^{2}+2^{2}}=2 \sqrt{2}(\mathrm{~cm})$.
Khối chóp tứ giác đều có chiều cao là: $\sqrt{3^{2}-\left(\dfrac{2 \sqrt{2}}{2}\right)^{2}}=\sqrt{7}(\mathrm{~cm})$.
Suy ra thể tích khối chóp tứ giác đều là: $V_{2}=\dfrac{1}{3} \cdot 2^{2} \cdot \sqrt{7}=\dfrac{4 \sqrt{7}}{3}\left(\mathrm{~cm}^{3}\right)$.
Số tiền mua kim loại dùng để làm thiết bị đó là: $2,5\left(6+\dfrac{4 \sqrt{7}}{3}\right) \approx 24$ (nghìn đồng).
Thể tích khối lăng trụ bằng diện tích đáy nhân với chiều cao.
Thể tích khối chóp tứ giác bằng $\dfrac{1}{3}\cdot$ diện tích đáy nhân với chiều cao.