Đề bài
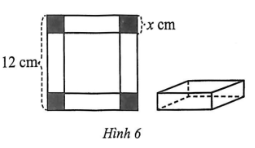
Cho một tấm nhôm hình vuông cạnh 12 cm , người ta cắt ở bốn góc bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x\left( {{\rm{\;cm}}} \right)$, rồi gập tấm nhôm lại như Hình 6 để được một cái hộp có dạng hình hộp chữ nhật không có nắp. Giá trị của $x$ bằng bao nhiêu centimet để thể tích của khối hộp đó là lớn nhất (làm tròn kết quả đến hàng đơn vị).
Phương pháp giải
+ Tìm điều kiện của $x$.
+ Tìm các kích thước của hình hộp.
+ Tính thể tích của hình hộp chữ nhật theo $x$.
+ Tìm giá trị lớn nhất của hàm số vừa thu được, từ đó rút ra kết luận.
Lời giải chi tiết
Ta thấy độ dài $x(\mathrm{~cm})$ của cạnh hình vuông bị cắt phải thoả mãn điều kiện $0 < x < 6$.
Sau khi cắt bốn cạnh của hình vuông và gập lai ta được hình hộp chữ nhật có các kích thước $12 - 2x (cm), 12 - 2x (cm), x (cm)$.
Thể tích hình hộp chữ nhật là: $V(x)=x(12-2x)^{2}=4\left(x^{3}-12 x^{2}+36 x \right)$.
Ta cần tìm giá trị lớn nhất của $V(x)$ với $0 < x < 6$.
Ta có $V^{\prime}(x)=4\left(3 x^{2}-24 x+36\right), V^{\prime}(x)=0 \Leftrightarrow x=2$ hoặc $x=6$.
Bảng biến thiên của hàm số $V(x)$ như sau:
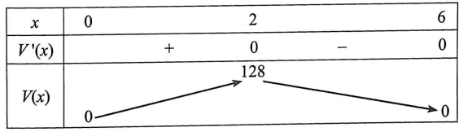
Căn cứ vào bảng biến thiên, ta thấy trên khoảng $(0 ; 6)$ hàm số $V(x)$ đạt giá trị lớn nhất bằng 128 tại $x=2$.
Vậy để khối hộp tạo thành có thể tích lớn nhất thì $x=2(\mathrm{~cm})$.
Cách giải bài toán tối ưu hóa đơn giản:
Bước 1: Xác định đại lượng Q mà ta cần làm cho giá trị của đại lượng ấy lớn nhất hoặc nhỏ nhất và biểu diễn nó qua các đại lượng khác trong bài toán.
Bước 2: Chọn một đại lượng thích hợp nào đó, kí hiệu là x, và biểu diễn các đại lượng khác ở Bước 1 theo x. Khi đó, đại lượng Q sẽ là hàm số của một biến x. Tìm tập xác định của hàm số $Q=Q\left( x \right)$.
Bước 3: Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số $Q=Q\left( x \right)$ bằng các phương pháp đã biết và kết luận.
📌 Ứng dụng của bài toán tối ưu hóa trong thực tiễn: Bài toán tối ưu hóa giúp chúng ta giải quyết những vẫn đề trong cuộc sống như tối đa hóa diện tích, khối lượng, lợi nhuận, cũng như tối thiểu hóa khoảng cách, thời gian, chi phí.
📊 Thực tế bài toán: Muốn tìm thể tích của hộp chữ nhật là lớn nhất, bài toán tối ưu hóa giúp ta giải quyết vấn đề này.